This year, after a hiatus that lasted a couple decades, I started playing Dungeons & Dragons again. I’m a bit late to the D&D renaissance – it has broken into the mainstream so thoroughly that it has appeared in a number of popular (read: target audience != nerds) TV shows. D&D is popular enough that I assume anyone reading this is familiar with the basics: players take on the role of heroes and collaboratively tell a story, using dice rolls to determine the success of their attempted actions.
The most common roll in D&D is using the result of a 20 sided die and comparing it to some pre-determined threshold value set by the dungeon-master (a sort of narrator/referee for the game). Your character’s chance of success isn’t left to being a coin flip: if they’re attempting something they’re good at, like a keen eyed elven archer shooting her bow, you’ll get to add a number to the die roll before comparing it to the target value. Likewise, if they’re attempting something they’re bad at, like a dim-witted orc trying to see through an illusion, you’ll have to subtract a number from the die roll. These added/subtracted numbers, called modifiers, have been used since the first version of D&D, played some 40 odd years ago. The most recent edition of D&D (5th edition, released in 2014) still uses modifiers, but it has also added a new twist: advantage and disadvantage.
Previously, everything was handled with modifiers: both the inherent abilities of your character and the circumstances of a particular moment. For example, the elven archer might get a +6 modifier on any attack made with her bow, and if she was attacking an unsuspecting victim who hadn’t noticed her yet, she might get an additional +4 modifier. Depending on the circumstances of a particular action, many different modifiers could apply, and you would add them all up to find the final modifier to use. In 5th edition, there are still modifiers, but they primarily apply to the inherent abilities of the hero. The circumstances of the particular action use a new system called advantage and disadvantage. Most checks will be made without advantage or disadvantage, and you simply roll the 20 sided die and add your inherent modifier. If the circumstances are favorable to your character’s success (e.g., the aforementioned bow-shooting while not being noticed), you can roll with advantage, which means you get to roll two 20 sided dice and take the higher value. If the circumstances are unfavorable, you roll with disadvantage, meaning that you roll two 20 sided dice and take the lower value.
The advantage system is more elegant, as you no longer need to determine a numerical modifier for each situation, you just decide if a situation calls for advantage, disadvantage, or neither. However, it’s also less flexible, as it can’t accommodate any subtlety between cases where advantage does apply. With positive modifiers, you can give +1, +2, +3, and beyond. With advantage, you either get advantage on the roll or you don’t.
When I first learned about this system, advantage seemed incredibly powerful to me, and like something that should be used sparingly. Getting to roll twice and choosing the higher value intuitively feels like you should almost always succeed! But as we’ll get to in the real meat of this post, that is not necessarily the case. Since this is ultimately all about probability, we can convert between advantage and an “effective modifier”, to see how much likelier advantage makes us to succeed on a roll.
The target value you are trying to beat (or match) with your roll is called a difficulty class, or DC. Without modifiers or advantage/disadvantage, it’s simple to calculate your chance of success. There are 20-DC sides that would beat the DC, and one side that would match it. A fair 20 sided die has an equal chance of landing on any of its 20 sides, so your chance of success is given by:
![]()
If we add in modifiers, it doesn’t complicate things much. A modifier of +3 means that there are three additional sides we can roll on that die that will lead to success, while a modifier of -2 means there are two fewer sides. So, adding this into our equation, we get:
![]()
We can see that changing the modifier by 1 changes the probability of success by 1/20, or 5%. This corresponds to the 20 sided die having a 5% chance of landing on any given side, and changing the modifier by 1 leading to one additional (or fewer) side of the die leading to success.
This makes it very easy to see how changing a modifier affects probability. Assuming that the DC is in the range where it will be possible for us to succeed or fail (i.e., it’s not extremely low like -4 or extremely high like 37), a +2 modifier will always improve our probability of success by 10%, and a -5 modifier will always decrease the probability of success by 25%.
To see how advantage and disadvantage affects our probability of success, it is helpful to define a more convenient version of DC. Instead, we’ll use an “effective DC”, which we calculate as EDC = DC – 1 – mod. This allows us to rewrite the equation above in a cleaner way:
![]()
And we can also calculate our chance of failure:
![]()
To calculate probabilities of rolls made with advantage or disadvantage, you need to understand the probabilities of independent events. Basically, the result of one roll doesn’t affect the result of the other roll – the two rolls can be treated as independent occurrences. When we roll with advantage, we get to choose the higher number, so to fail when rolling with advantage, it’s like we would need to fail twice in a row. The probability of failing twice in a row is just the probability of failing once times the probability of failing once:
![]()
and thus the probability of success is just 1 minus the result above:
![]()
With advantage, we’re squaring the fraction that we subtract from 1, so clearly we have a greater chance of success, but it’s not as simple as the case with modifiers, where we could say that changing the modifier by 1 changes the chance of success by 5%. There’s no fixed change with advantage, it depends on your original chance of success.
(Note: you can do a similar calculation for disadvantage, but in that case the chance of success w/ disadvantage is chance of success squared and chance of failure with disadvantage is 1 – chance of success squared. For the rest of this post I’ll only work through examples with advantage, but the same principles apply to disadvantage.)
We can see the varying benefit of advantage in practice by looking at some sample EDCs. Let’s first consider the very difficult EDC of 18 (meaning you’d need to roll a 19 or 20 to succeed). Without advantage, the probability of success is 10%:
![]()
With advantage, the probability of success is 19%:
![]()
Thus, advantage improved our chance of success by 9%, which corresponds roughly to a modifier of +2 (which would give us a bonus of 10%).
Next, let’s look at the case of an easier EDC of 8 (meaning you’d need to roll 9 or higher to succeed). Without advantage, the probability of success is 60%. With advantage, the probability of success is 84%. Thus, advantage increased our odds of success by 24%, corresponding roughly to a modifier of +5.
As it turns out, the increase in probability of success is greatest for moderate EDC values. With a very high DC, you are still likely to fail even with advantage, and with a low DC you are likely to succeed even without advantage, so the addition of advantage doesn’t change the probabilities much. But if you have a roughly 50% chance of success, adding an extra attempt is the most valuable. You can see the equivalent modifier when you have advantage based on EDC in the plot below:
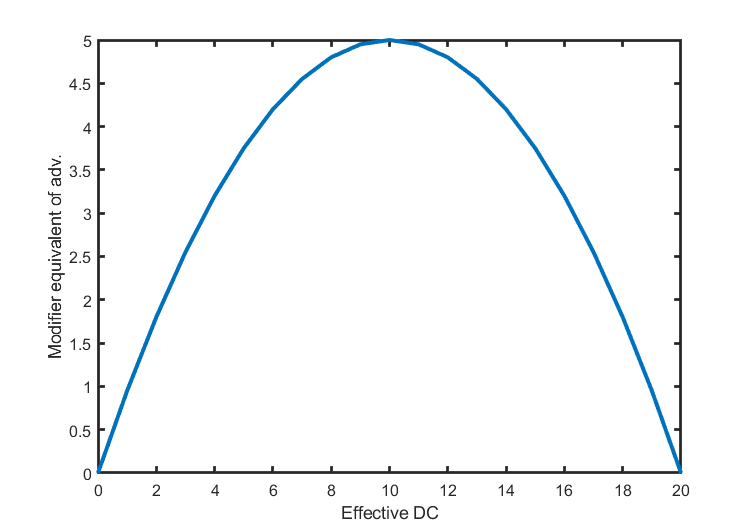
From this we can see that advantage can be equivalent to a +5 modifier, which is quite strong, but that advantage is capped, and it’s less powerful than my intuition originally suggested. So while I definitely could have had plenty of fun playing D&D without having thought through this math, it has let me grant advantage (or impose disadvantage) on rolls without being worried that it’s “overpowered”.
Thank you so much for this, Lee. It was extremely helpful. I wonder if you could enlighten me further.
I am currently designing an RPG and I’m trying to sort out some mechanics similar to this. The difference being that the player will roll 2 x 6 sided dice (2d6) instead of a 20 sided die. And also, they would only roll an extra 1d6, for the advantage/disadvantage die. The player would roll all 3 dice and take the lowest or highest 2 of the 3 dice….discarding the 3rd.
It would definitely be different from the above blog post because I’m not doubling the die roll (only 3d6, not 4d6), so I don’t believe the results would be the same. If you are so inclined, I would love to know how this method would stack up to standard modifiers.
Thank you for your time.
Here are the results assuming you want to roll high. Hopefully this “table” that I make will be legible in this comment. The first column is the number you are trying to roll (e.g., 5 means you want to roll a 5 or higher), the second column is the approximate chance of success rolling 2d6, and the third column is the approximate chance of success rolling 3d6 and dropping the lowest value.
3 —– 97.2% —– 99.5%
4 —– 91.7% —– 98.1%
5 —– 83.3% —– 94.9%
6 —– 72.2% —– 89.4%
7 —– 58.3% —– 80.6%
8 —– 41.7% —– 68.1%
9 —– 27.8% —– 52.3%
10 —- 16.7% —– 35.6%
11 —- 8.3% —— 19.9%
12 —- 2.8% —— 7.4%
You can find the standard modifier comparable to giving advantage by finding two situations with similar chance of success. For example, suppose you are trying to roll a 7 or higher. Under normal conditions, you have a ~58% chance to do so. With advantage, this increases to ~81%. An 81% chance of success is roughly the same as rolling 5 or higher without advantage. That means that in this case, advantage is worth roughly the same as a +2 modifier (since 5 and 7 differ by 2).
Your system is similar to standard D&D5e in that it benefits middle difficulty rolls the most, and gives less of an advantage on very easy or very hard rolls. The magnitude is much different though — in your system, giving advantage seems to correspond to a standard modifier ranging from +1 to +2.
Hi Lee,
I think this interpretation of what modifier is compared to advantage/disadvantage is the most usefull interpretation. I would like to add that on avarage advantage/disadvantage adds or subtracts respectively 3.25 to a roll. You can calculate this by deriving a discrete probabillity mass function and calculate its expectation. To verify this expectation, one can simulate this process using code.
Kind regards,
Koen