Category: Gaming

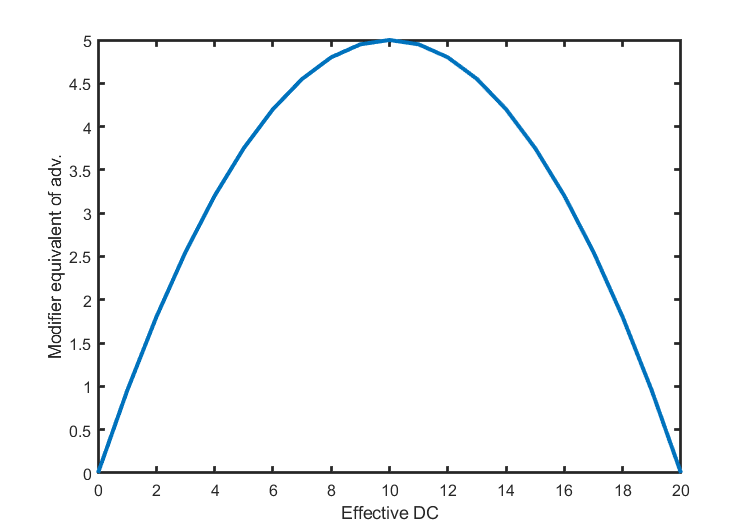
In my last post on D&D, I wrote about differences in the probabilities of the success of ability checks using modifiers (an old system) compared to advantage/disadvantage (a newer system). That was a pretty innocuous topic, since it was just applying math to different ways of interpreting dice rolls. In this post, I wanted to explore a potentially more controversial topic: the probabilities of opposed checks. This is potentially controversial because it gets a bit into the question of whether certain aspects of D&D are “realistic enough”, which some people might argue is an important question, since the universe of D&D is governed by many of the same physics as our own universe, while other people might argue the opposite because D&D is fundamentally a fantasy game. In any case, I’m still interested in the math, so hopefully my results don’t make any D&D players with strong opinions upset.

With a normal ability check, you roll a 20 sided die (“d20” for short) add modifiers, and compare the result to a fixed number. (If you have advantage or disadvantage on the check, you roll 2 d20s instead and take the higher or lower number, respectively.) For example, an easy task might require that your roll plus modifiers be 10 or higher, while a very difficult task might require that your roll plus modifiers be greater than 25.

In an opposed check, two characters are pitted against each other, so instead of needing your roll to beat a fixed number, the winner of an opposed check is whoever rolls highest after modifiers have been applied. A common example of an opposed check is when one character attempts to grapple another character: the two players involved make an opposed athletics check, and if the instigator rolls higher, they have successfully grappled the other character.

We can represent the probability of different outcomes visually. Each player rolls a d20, which means that there are 20*20 = 400 possible outcomes, which we can lay out in a grid. In the simple case where both players have the same modifier for the check, if they roll the same number the result is a tie (grey squares in the chart below), if player 1 rolls higher they win (blue squares in the chart below), and if player 2 rolls higher they win (red squares in the chart below).

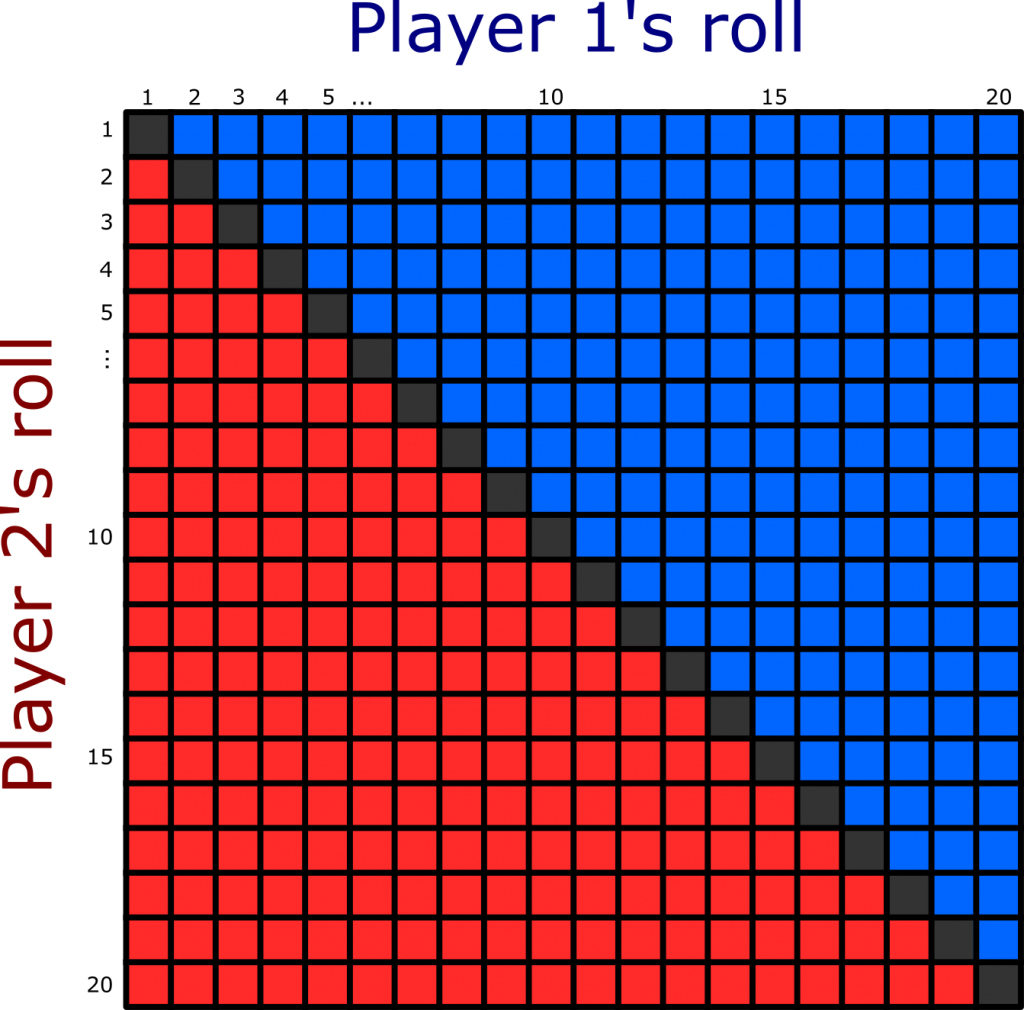
The relative area of each color tells us the probability of that outcome. For simplicity, we’ll treat the grey squares as being half red and half blue (depending on the exact situation/house rules being used, a tie could lead to either player “winning” the opposed check). For the situation above, the area is then half red and half blue, matching our expectations that evenly matched characters should have a 50% chance of winning.

However, for mismatched characters, the probabilities might not be quite what you’d expect. A warrior with a high starting strength score (i.e., not boosted by magical spells or special items) who is proficient at grappling might have a modifier of +6 on their check. They could attempt to grapple a wizard with unremarkable strength who is not trained at grappling, corresponding to a +0 modifier on their check. In this case, (with player 1 being the warrior) the line dividing the areas will move down by 6 places, since the warrior’s modifier is +6 compared to the wizard.

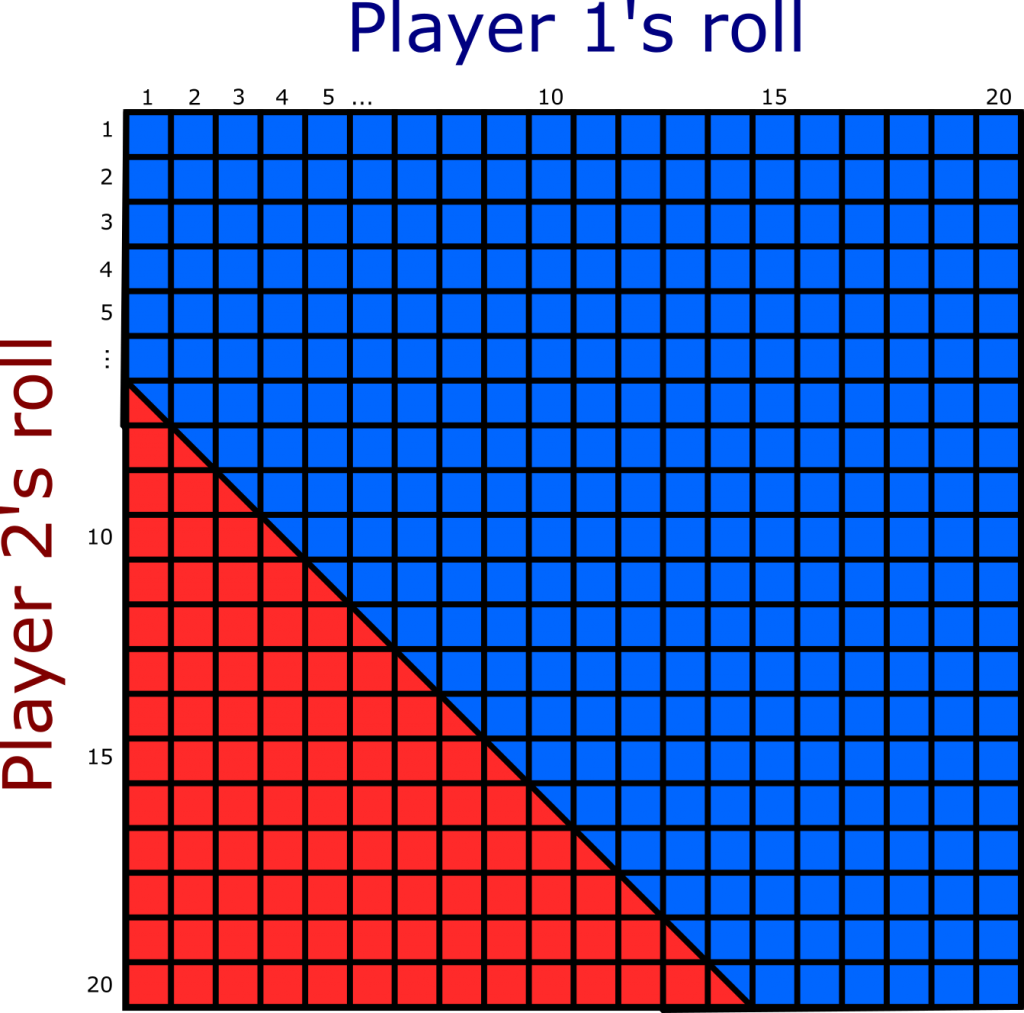
The total area of the chart is 20*20 = 400, while the area of the wizard’s triangle is now 1/2*14*14 = 98. That means that even though the warrior is built entirely around being strong (and good at grappling), and the wizard has no specialization in grappling, the wizard will still be successful 98/400 times – a roughly 25% chance of winning the opposed check.

We can remedy this a bit if the warrior has advantage, but the wizard still might have a better chance than you expect. In this case, the warrior gets to roll twice and choose the higher roll, so there are three d20s being rolled in total, for 20*20*20 = 8000 possible outcomes. We can represent the new chart as a cube, with each edge corresponding to one of the d20 rolls. For the wizard to succeed, they’ll need to roll higher than both of the warriors rolls (after accounting for the modifier), so there’s just one corner of the cube of possibilities that corresponds to their success:

The volume of the wizard’s corner of the cube is 1/3*14*(1/2*14*14) = 457, so the ratio of that corner to the total cube volume corresponds to 457/8000, or a roughly 6% chance of success. This probably matches our expectations of reality much better, but it’s still a decent chance for the wizard to succeed – better than some lopsided boxing odds, for example, even though in that case both fighters will still be professionals.

For many D&D players, this analysis is completely worthless, because a lot of the entertainment of D&D comes from the high variance and wacky, unexpected situations. But it does tell us something useful for players who enjoy a game that’s more grounded in reality. For situations that shouldn’t depend much on variance, you might not want to call for a die roll at all (e.g., in an arm wrestling match, a character with 2+ strength more than the other character could win automatically, unless the weaker character cheats). And even in situations that do have some variance, you may want to grant the character with the higher modifier advantage more readily than normal, so that the associated probabilities match something closer to what we’d expect.

This year, after a hiatus that lasted a couple decades, I started playing Dungeons & Dragons again. I’m a bit late to the D&D renaissance – it has broken into the mainstream so thoroughly that it has appeared in a number of popular (read: target audience != nerds) TV shows. D&D is popular enough that I assume anyone reading this is familiar with the basics: players take on the role of heroes and collaboratively tell a story, using dice rolls to determine the success of their attempted actions.

The most common roll in D&D is using the result of a 20 sided die and comparing it to some pre-determined threshold value set by the dungeon-master (a sort of narrator/referee for the game). Your character’s chance of success isn’t left to being a coin flip: if they’re attempting something they’re good at, like a keen eyed elven archer shooting her bow, you’ll get to add a number to the die roll before comparing it to the target value. Likewise, if they’re attempting something they’re bad at, like a dim-witted orc trying to see through an illusion, you’ll have to subtract a number from the die roll. These added/subtracted numbers, called modifiers, have been used since the first version of D&D, played some 40 odd years ago. The most recent edition of D&D (5th edition, released in 2014) still uses modifiers, but it has also added a new twist: advantage and disadvantage.

Previously, everything was handled with modifiers: both the inherent abilities of your character and the circumstances of a particular moment. For example, the elven archer might get a +6 modifier on any attack made with her bow, and if she was attacking an unsuspecting victim who hadn’t noticed her yet, she might get an additional +4 modifier. Depending on the circumstances of a particular action, many different modifiers could apply, and you would add them all up to find the final modifier to use. In 5th edition, there are still modifiers, but they primarily apply to the inherent abilities of the hero. The circumstances of the particular action use a new system called advantage and disadvantage. Most checks will be made without advantage or disadvantage, and you simply roll the 20 sided die and add your inherent modifier. If the circumstances are favorable to your character’s success (e.g., the aforementioned bow-shooting while not being noticed), you can roll with advantage, which means you get to roll two 20 sided dice and take the higher value. If the circumstances are unfavorable, you roll with disadvantage, meaning that you roll two 20 sided dice and take the lower value.

The advantage system is more elegant, as you no longer need to determine a numerical modifier for each situation, you just decide if a situation calls for advantage, disadvantage, or neither. However, it’s also less flexible, as it can’t accommodate any subtlety between cases where advantage does apply. With positive modifiers, you can give +1, +2, +3, and beyond. With advantage, you either get advantage on the roll or you don’t.

When I first learned about this system, advantage seemed incredibly powerful to me, and like something that should be used sparingly. Getting to roll twice and choosing the higher value intuitively feels like you should almost always succeed! But as we’ll get to in the real meat of this post, that is not necessarily the case. Since this is ultimately all about probability, we can convert between advantage and an “effective modifier”, to see how much likelier advantage makes us to succeed on a roll.

The target value you are trying to beat (or match) with your roll is called a difficulty class, or DC. Without modifiers or advantage/disadvantage, it’s simple to calculate your chance of success. There are 20-DC sides that would beat the DC, and one side that would match it. A fair 20 sided die has an equal chance of landing on any of its 20 sides, so your chance of success is given by:

If we add in modifiers, it doesn’t complicate things much. A modifier of +3 means that there are three additional sides we can roll on that die that will lead to success, while a modifier of -2 means there are two fewer sides. So, adding this into our equation, we get:

We can see that changing the modifier by 1 changes the probability of success by 1/20, or 5%. This corresponds to the 20 sided die having a 5% chance of landing on any given side, and changing the modifier by 1 leading to one additional (or fewer) side of the die leading to success.

This makes it very easy to see how changing a modifier affects probability. Assuming that the DC is in the range where it will be possible for us to succeed or fail (i.e., it’s not extremely low like -4 or extremely high like 37), a +2 modifier will always improve our probability of success by 10%, and a -5 modifier will always decrease the probability of success by 25%.

To see how advantage and disadvantage affects our probability of success, it is helpful to define a more convenient version of DC. Instead, we’ll use an “effective DC”, which we calculate as EDC = DC – 1 – mod. This allows us to rewrite the equation above in a cleaner way:

And we can also calculate our chance of failure:

To calculate probabilities of rolls made with advantage or disadvantage, you need to understand the probabilities of independent events. Basically, the result of one roll doesn’t affect the result of the other roll – the two rolls can be treated as independent occurrences. When we roll with advantage, we get to choose the higher number, so to fail when rolling with advantage, it’s like we would need to fail twice in a row. The probability of failing twice in a row is just the probability of failing once times the probability of failing once:

and thus the probability of success is just 1 minus the result above:

With advantage, we’re squaring the fraction that we subtract from 1, so clearly we have a greater chance of success, but it’s not as simple as the case with modifiers, where we could say that changing the modifier by 1 changes the chance of success by 5%. There’s no fixed change with advantage, it depends on your original chance of success.

(Note: you can do a similar calculation for disadvantage, but in that case the chance of success w/ disadvantage is chance of success squared and chance of failure with disadvantage is 1 – chance of success squared. For the rest of this post I’ll only work through examples with advantage, but the same principles apply to disadvantage.)

We can see the varying benefit of advantage in practice by looking at some sample EDCs. Let’s first consider the very difficult EDC of 18 (meaning you’d need to roll a 19 or 20 to succeed). Without advantage, the probability of success is 10%:

With advantage, the probability of success is 19%:

Thus, advantage improved our chance of success by 9%, which corresponds roughly to a modifier of +2 (which would give us a bonus of 10%).

Next, let’s look at the case of an easier EDC of 8 (meaning you’d need to roll 9 or higher to succeed). Without advantage, the probability of success is 60%. With advantage, the probability of success is 84%. Thus, advantage increased our odds of success by 24%, corresponding roughly to a modifier of +5.

As it turns out, the increase in probability of success is greatest for moderate EDC values. With a very high DC, you are still likely to fail even with advantage, and with a low DC you are likely to succeed even without advantage, so the addition of advantage doesn’t change the probabilities much. But if you have a roughly 50% chance of success, adding an extra attempt is the most valuable. You can see the equivalent modifier when you have advantage based on EDC in the plot below:

From this we can see that advantage can be equivalent to a +5 modifier, which is quite strong, but that advantage is capped, and it’s less powerful than my intuition originally suggested. So while I definitely could have had plenty of fun playing D&D without having thought through this math, it has let me grant advantage (or impose disadvantage) on rolls without being worried that it’s “overpowered”.

Even though the arrival of summer no longer corresponds to a long break from school/work for me, it still reminds me of the weeks spent at summer camp when I was growing up. In my elementary school years, one of my favorite games to play at camp was capture the flag (CTF). There’s something deeply compelling about the large scale of the game, and the teamwork and coordination required to win. After playing for many summers, however, I started to realize that there are some big problems with the mechanics of the “classic” version of CTF. Perhaps it was from playing more video/board games and looking at the summer camp staple from a game design perspective, but at some point I became convinced that there should be many ways to improve on the classic version of capture the flag.

“Classic” Capture the Flag

I imagine most people reading this are familiar with capture the flag, but there are enough variations that it is still worth defining what I consider the classic version and the rules for the majority of the games I played in. The game is played on a large open field divided in half, with each of the two teams taking one half of the field as their “home” side. Each team has a flag on their side that the other team is trying to retrieve and bring back to their own side. Successfully retrieving the flag earns your team a point (or wins the game outright, if you’re not playing for a fixed time). If you are tagged by an opposing player while on their side of the field, you go to a “jail” on the opponents’ side of the field. Players in jail are freed if a non-jailed player from their team tags the jailed players. The players in jail can form a chain by holding hands in order to stretch further from the jail spot to make it easier for teammates to free them. There is a “safe zone” around the flag spot, so that if you reach the flag, you can take a breather without being tagged before trying to run the flag back to your own side.

The fundamental issue I have with this standard version of capture the flag is that the optimal strategy is very defensive, and results in slow, war of attrition type game play. In any game of CTF, you need to distribute your resources (players) between offense (trying to capture the opposing flag or free your jailed players) and defense (protecting your flag and keeping opposing jailed players from being freed). Sending players to try to capture the flag is risky: either you succeed and win, or you fail and some of your players are jailed. If you have a lot of fast players, then you’re likely to succeed, but for balanced teams, the chance of success of any given attempt is pretty low. Thus, sending players on offense at the beginning of a round is generally a bad strategy. It is better to play defensively until you’ve jailed enough of the opposing players that their defenses are stretched thin and you have a higher chance of capturing their flag. Unfortunately, if both teams adopt this strategy, then CTF becomes a game of sitting around and waiting more than anything else, which is no fun for either team.

I haven’t played capture the flag since undergrad, so maybe my theory-crafting about it so many years later misses the mark of what it’s actually like to play, but in any case, all these years have given me the opportunity to come up with many variations on the classic game that address what I view as the fundamental flaw of the game.

Variations on Jail

Jail is probably the most problematic aspect of CTF, as it’s basically player elimination, one of the most infamous game design mechanics out there. Perhaps as a consequence of this, there are plenty of variations on the typical jail rules, and jail is the main aspect of the game where I’ve seen different rules actually implemented at summer camp. All the variations below are ways of making it easier to get out of jail, which discourages strategies that depend on keeping lots of opposing players in jail.

A simple variation, and one I considered adding as part of the classic rules since I think it is fairly common, is that jailed players who manage to tag an opposing player free their team. This discourages “jail guards” from staying too close to the jail, and gives jailed players something more to do, as when they are linked they can coil up and stretch out to try to catch opposing players off guard and tag them.

Another variation is to give jailed players an alternate task in order to release themselves. It could be something physical (do X pushups, do Y jumping jacks) or it could be something mental (solve a Rubik’s cube, solve a Sudoku puzzle). Assuming the players are capable of completing the assigned task, this puts a time limit on how long players will stay jailed, and give them something to do in the meantime.

An even simpler way of assuring that players don’t stay in jail for too long is to have regular “jailbreaks”, when all players are released from both jails. Short intervals (releasing players every 2 minutes) ensure that the game stays fast paced, as players will never spend too long in jail, while longer intervals (releasing players every 10 minutes) doesn’t change the game drastically, but guarantees that players won’t be in jail all afternoon.

The most dramatic change to the rules would be to get rid of jail altogether. The point of jail is to be a negative consequence for being tagged, but you don’t necessarily need a jail to achieve this. An example of an alternative is that rather than tagged players being jailed, tagged players must walk back to their own side (or maybe their own flag safe zone) with their hands on their head until they’re allowed to resume play. Getting rid of jail essentially eliminates downtime, so everyone gets to play for the entirety of the game, and there is little disincentive from sending players to try to capture the opposing flag.

Variations on Field of Play

While it’s not always an easy change to implement, one option that can help push the balance of play towards offense rather than defense is changing where the game is actually played. Rather than an open field, where everyone can see what’s going on and quickly respond to defend when their flag is being threatened, CTF can also be played in a forest or on a campus with buildings between the flags. Obstacles like trees and buildings give players something to hide behind, so there are opportunities to steal a flag through distraction and stealth, rather than just by running faster than the other players.

Another option, if you’re limited to playing on an open field, is to make the sides more complex than just a field cut in half (although you’d probably need a lot of cones/rope to mark the sides in this case). On the classic field, teams only need to worry about opponents coming from a single direction. But if the shape of the two home sides were interdigitated “L”s or “U”s, for example, then flag guards would need to worry about players coming from two or three directions, making the flag harder to guard and making capture attempts more likely to succeed.

Variations on the Flag

Another option for variation is to change the rules around the flag itself. In the classic version of the game, the flag can be handed off, but it can’t be thrown – if not due to the rules, then simply because flags are generally difficult to throw. If the flag is replaced by a ball or a frisbee, then allowing the flag to be thrown between teammates (as long as it doesn’t touch the ground) opens up new offensive strategies. In order to keep it possible to defend against the thrown flag, it’s probably prudent to disallow throws to or from safe zones. For example, you would need to step outside the safe zone around the flag to throw, and you couldn’t throw it to a teammate on your side of the field’s dividing line.

Another change that would open up the field of play would be to have multiple flags on each side. This would naturally make it harder for a team to defend all of its flags effectively, and you could additionally assign different point values to the different flags, which would add a layer of strategy to the game. For example, a flag that is close to the dividing line might be worth just 1 point, while a flag that is deep on the opponent’s side and doesn’t include a safe zone around it might be worth 5 points.

Variations on the Tag Method

Classic capture the flag is played with one hand touch, which means you just need to touch an opposing player with one hand (or really even just one finger) in order to get them out. A simple change to make it harder to defend and easier to capture the flag would be to use two hand touch, which requires you to tag an opposing player with both your hands simultaneously in order to get them out. In practice however, this variation might not work well, as I suspect it would lead to more arguments about whether or not someone was really tagged out (and classic CTF already has enough of those arguments).

Another variant is to use waist flags (like those used for flag football) that must be pulled in order to get a player out. In theory, this should make it more clear cut about whether a player was tagged out or not, but with the added possibilities of a player blocking their own flags with their hands or a flag falling out on its own, it’s unlikely that this method would eliminate accusations of cheating.

When Hearthstone, Blizzard’s take on a collectible card game, first came out, I was hooked. It tapped into my nostalgia for all the Magic: The Gathering I played when I was younger, but offered a much smoother playing experience than what was available for other online “card” games at the time. I played for a few years, but eventually grew bored of Hearthstone. Now I’m back on the online CCG bandwagon with the release of Magic: The Gathering Arena, the new Hearthstone-ified version of the original TCG/CCG.

Playing an online CCG again reminded me of one thing that never really made sense to me about Hearthstone: the way its ranked ladder worked. Most competitive online games use some variant of the Elo rating system. In such a system, each player has a number which corresponds to their skill level – whenever they win a game, that number goes up, and whenever they lose a game, that number goes down. The magnitude in the change of Elo rating is equal for the two players involved in the game (e.g., if I lose to you and consequently lose 5 points, that means you would gain 5 points) and depends on the difference in rating between the players. For example, if a player beats a much lower rated player, they will only get a small increase in rating, but if they lose to that much lower rated player, they will experience a large decrease in rating. Typically this Elo rating is then translated into a rank/tier/division, which broadly groups players by skill level. For example, in Rocket League, the lowest ranked players are Bronze, followed by (in ascending order): Silver, Gold, Platinum, Diamond, Champion, and Grand Champion.

Hearthstone, Magic Arena, and most online “card” based games don’t seem to follow this method, at least not until you get to the very top tier of the ladder (e.g., “Legendary” for Hearthstone, or “Mythic” for Magic). For the portion of the ladder relevant to most players, you start at (or near) the lowest rank at the beginning of every month, a win gets you one “point” (the exact terminology varies game to game), a loss loses you one point, and there are regular point cutoffs associated with each rank (e.g., each subsequent rank requires 5 more points than the last one). There are some specific caveats to each game, but that general system forms the foundation of the ranking system.

At the surface, it might seem like there’s not really a difference between these two systems. Both systems are zero-sum: any points lost by one player are gained by another. And assuming there are enough players so that you’re always playing someone of roughly your same skill level, then the importance of each game is about the same. What is different is the shape of the distribution of player skill ratings, which matters because in the card game system, this distribution is fundamentally connected to player ranks.

In the Elo system, the distribution tends to resemble a Bell curve, since each game should have roughly 50% chance of going either way, like a Galton Board. However, this distribution isn’t particularly important, since the developers can set arbitrary cutoff points for each rank. Given that the Gold and Platinum ranks are in the middle of the possible Rocket League ranks, players expect that an average player would be Gold or Platinum, and the Rocket League developers can set the ratings corresponding to Gold and Platinum to be in the middle of the distribution. If they found that players were happier when they were classified as a higher rank, they could arbitrarily shift the ratings so that Diamond corresponded to the middle of the distribution, without changing how the Elo rating system works overall.

The card game system would also resemble a Bell curve if it was truly zero-sum, but at the bottom of the ladder it is not actually zero-sum. Someone with zero points can’t lose points, so games at the bottom of the ladder result in a net positive production of points. By preventing players from going below zero points, the ranking distribution looks asymmetric and long-tailed, like a Pareto distribution, or a Chi-squared distribution with only one or two degrees of freedom. (Since this can be modeled as a diffusion process, I think of it as being like the temperature distribution in the heating of a semi-infinite solid.) The shape of this distribution wouldn’t matter if the developers set ranking cutoffs arbitrarily, but by keeping the point cutoffs regular or mostly regular, this long tailed distribution in points leads to a long tailed distribution in player ranks as well.

Since I’m sure most players don’t spend as much time thinking about distributions as I do, the card game ranking system becomes problematic because the perception of players’ rankings greatly differs from the reality of the ranking distribution. Back when I played Hearthstone, the effective lowest rank (corresponding to zero points in my above description) was 20, and the highest rank was 1. Consequently, a player might reasonably assume that an average skill level would get them to rank 10 or 11, when in fact, due to the skewed distribution, the median player might be at only rank 17 or 18.

So if you’re committed to this “card” ranking system, with its skewed distribution, what can you do? There are some changes that were built into the original Hearthstone system, like not having completely regular point cutoffs. For Hearthstone, the lowest ranks require 3 points to advance, while the highest ranks require 5 points. This helps spread out the lower ranks a bit more, but is not aggressive enough to really make the ranks match player expectations, and doesn’t address the fundamental problem that points are only created at the bottom of the ladder, and must funnel all the way up the ladder for more players to reach the highest ranks.

The big change I’ve noticed in Magic Arena is that there are way more instances of net positive point distribution. Hearthstone originally only had two sources of net point increase: a player losing at the bottom of the ladder when they couldn’t actually lose a point (but their opponent still gained one) and “win streaks,” where 3+ wins in a row would lead to more than one point per win. (Technically a ladder player beating a Legendary player also resulted in a net gain in points, but this would probably cancelled out by ladder players losing to Legendary players.) In Magic Arena, they added multiple “checkpoints” throughout the ladder, so that once you achieve a certain rank you can’t fall below it. These artificial floors add more net points to the system, since losing at the bottom of the ladder OR any checkpoint will result in a net increase in points (note: I believe Hearthstone implemented a similar change after I stopped playing). The other change is that in lower ranks, every single game is net positive: the winner gets two points and the loser only loses one. Between these changes, I suspect that the ranking distribution for Magic Arena players is much closer to player perception than it was for the original Hearthstone ladder.

All this discussion of how to specifically craft this card game ranked ladder system so that it matches player perceptions/expectations begs the question: why bother? Why not just adopt the Elo rating system used in other games? If you asked the developers of these games, I imagine that they would make an argument about transparency, since it’s much clearer what a player needs to do to advance: “win X more games than I lose”, compared to “gain X Elo rating points (which are often hidden from the player)” in other games. But I believe the real reason is to drive participation. By starting players at or near the bottom of the ladder every month, it forces them to play a decent number of games every month in order to achieve the rank they’re striving for. Free to play games (which basically all of these cards games are) need high participation rates to survive, and these ladder systems allow playing to always be associated with advancement (if perhaps in a more Sisyphean way than the developers would admit).

It should be readily evident from some of my other posts that I love Rocket League. I started playing ranked matches during Rocket League’s Season 3 (which ran from June 2016 through March 2017), and towards the end of August 2016 I started tracking my progress in a spreadsheet. I kept track of my skill ratings (similar to an Elo ranking) in the different playlists using a stat tracking website and once a week I would run through each of the default all-star trainings five times as an alternative metric for mechanical skills.

I had originally had very ambitious plans for what I would do with the stats I collected, but since it’s been two months since Season 3 ended I wanted to post something before the project lost all momentum. Perhaps I’ll revisit this in more detail later, but for now the project has culminated in a simple page posted here which lets you explore different ratings/rankings over time or number of games played.

There are a few points I found interesting from exploring the data:

• My unranked rating (rating from playing in casual playlists) stayed more or less constant over all of Season 3, even though I undoubtedly improved over that time period.
• Looking at a playlist rating vs. number of games played (e.g., Standard rating vs. Ranked standard games played) I hit a plateau in Duel and Solo standard, but not in Doubles or Standard. Perhaps through the latter half of Season 3, my teamwork improved more than other mechanical skills, which doesn’t show up as much in Duel or (unfortunately) in Solo standard.
• I plateaued fairly quickly in Keeper and Striker training, while I continuously improved in Aerial training. Keeper plateaued because I quickly approached 100% completion, whereas Striker seemed to always hover around 70%. I’m not sure why I’m not better at Striker even after spending so much time on it.

This Halloween my girlfriend Jaimie and I dressed up as Rocket League cars. She doesn’t play, but I was set on the costume and she wanted her costume to match mine:

We made them ourselves, so ideally I would’ve thoroughly documented the process, but we were a bit rushed for time, since we just worked on them during evenings of the week leading up to Halloween. Instead I just took pictures intermittently, which you can see below. As you can see, the cars are primarily made of taped together cardboard that we painted. The wheels and tires are attached to the main body with toothpicks and superglue.

A few weeks ago, at the recommendation of a friend, I started playing Rocket League. In Rocket League you control a rocket powered car in a game resembling indoor soccer: you score points by knocking a ball into the opposing team’s goal, and you try to prevent the other team from knocking the ball into yours. While I’m late to the party (Rocket League has been out for a bit over a year now), in these past few weeks it’s completely won me over: right now I’d say I’m spending the majority of my free time playing Rocket League.

I’ve also been playing some actual soccer this summer, and after playing soccer one day I realized why Rocket League is so compelling to me. Rocket League is the most authentic soccer video game I’ve ever played. A natural response might be: “That’s ridiculous! How could a game about cars playing soccer be more authentic than games like FIFA, which are about the actual sport of soccer?” I would not contest that watching a game played out in FIFA is more like watching an actual soccer game, but playing Rocket League captures the feeling of actually playing soccer better than any other video game I’ve played. I am not the first person to share this opinion, but nonetheless I thought I’d take this entry to explain my reasoning in a bit more depth.

The first reason is that the mechanics of Rocket League make the experience much closer to playing soccer. In an actual soccer game, when you want to shoot, pass, or clear the ball, all of these are accomplished by kicking the ball with your foot (well, usually contact is with the foot, but occasionally it could be with the leg, head, etc.). In FIFA-like video games, you perform the different kicks by pressing different buttons, e.g., [x] to pass or [y] to shoot, even though an actual soccer player kicks the ball in both cases, just in a different way. In Rocket League, the “kicks” are collisions, and all the contact between the car and the ball is physically simulated in the game. So whether you want to pass or shoot, in both cases you need to drive your car into the ball. Whether it’s a pass or a shot depends on how fast you strike the ball and at what angle, there’s no pass button you can press that will cause your car to knock the ball towards a teammate.

The result of these mechanics is that when you’re bearing down on a ball in front of the opponent’s goal in Rocket League, it feels like running up to shoot the ball in actual soccer. In both cases you’re acutely focused on how to strike the ball to maximize the chance of it going into the goal. In FIFA, on the other hand, you just press the “shoot” button and hope for the best (I’m probably underselling the control in FIFA a bit here, but you get the idea). Likewise, in Rocket League when you’re trying to clear a ball in front of your goal, you’re trying to get some part of the car between the goal and ball (similar to real soccer, but replace car with leg), not just mashing the “clear” button in the proximity of the ball.

The other big reason that Rocket League recreates an authentic soccer experience is the perspective. While not technically played in a 1st person view, Rocket League is 1st person in the sense that you only control one car, and your field of vision is limited to originating from around where that car is. This is different from FIFA-like games, which let you swap control of players so you’re typically in control of the player with the ball (on offense) or the player challenging the ball (on defense), and are viewed from a perspective similar to how professional soccer games are broadcast, so you can see all the relevant action around the ball.

In a real soccer game, what you do off the ball is very important: your position is critical to creating scoring opportunities for your team and shutting down chances for your opponent. This aspect of team play is largely out of your control in FIFA-like games: what the other players do on your team is automated. In Rocket League, since you only control your own car, you need to decide where to position yourself for the entire game, not just when you’re on the ball. And similar to real soccer, this positioning is very important: if you play like a 5-year-old plays soccer and just chase the ball the whole match, your team won’t have the structure to both attack and defend, and you’ll doom yourself to many losses.

The view that Rocket League is played in (psuedo 1st person) also makes the experience more authentic. In real soccer, situational awareness is an important skill to have, which is recreated in Rocket League by necessitating that you pan the camera up and down the field if you want to know where your teammates and opponents are. In FIFA-like games, the positions of everyone is simply laid out for you by the high viewing angle of the field. The Rocket League view also means you need to actually be able to judge distances and trajectories to know where you should head to intercept a ball or player (as in real soccer), whereas FIFA-like games put a glyph on the ground where the ball is going to land, since it would be intractable to assess a ball trajectory from the high viewing angle they use.

To me, this combination of mechanics and perspective end up making Rocket League so much more fun because it feels like actually playing soccer. In Rocket League it feels like you scored the goal, whereas in FIFA it feels like the character in the game scored, you just happened to tell him to shoot.